Model properties

A simplified analysis model of a membrane type Normal is presented in the table below. When applying nonlinear relation between force and strain it is recommended to validate the input data on a simple model, like the one presented here.

Description	Abbreviation	Value
Height of membrane panel [m]	H	10
Width of membrane panel [m]	W	10
Thread diameter [m]	d	0.002
Weight in water [kg]	m	0
Maskwidth Y (distance between threads) [m]	\(\text{Lm}_Y\)	1
Total length of therads in vertical direction (Z) [m]	\(L_Z\)	100
Number of vertical threads [-]	\(\#_Z\)	\(\frac{L_Z}{W} = 10\)
Pointload per membrane panel corner [N]	\(P_Z\)	-12500
Force per vertical thread [N]	\(F_Z \)	\(\frac{2 \cdot P_Z}{\#_Z} = -2500\)

The figure below illustrates the model, which is restrained in the two top nodes. Two point loads are added to the lower nodes, each -12 500 N.

To view the properties of the membrane, doble click on Membrane panel in the components window.

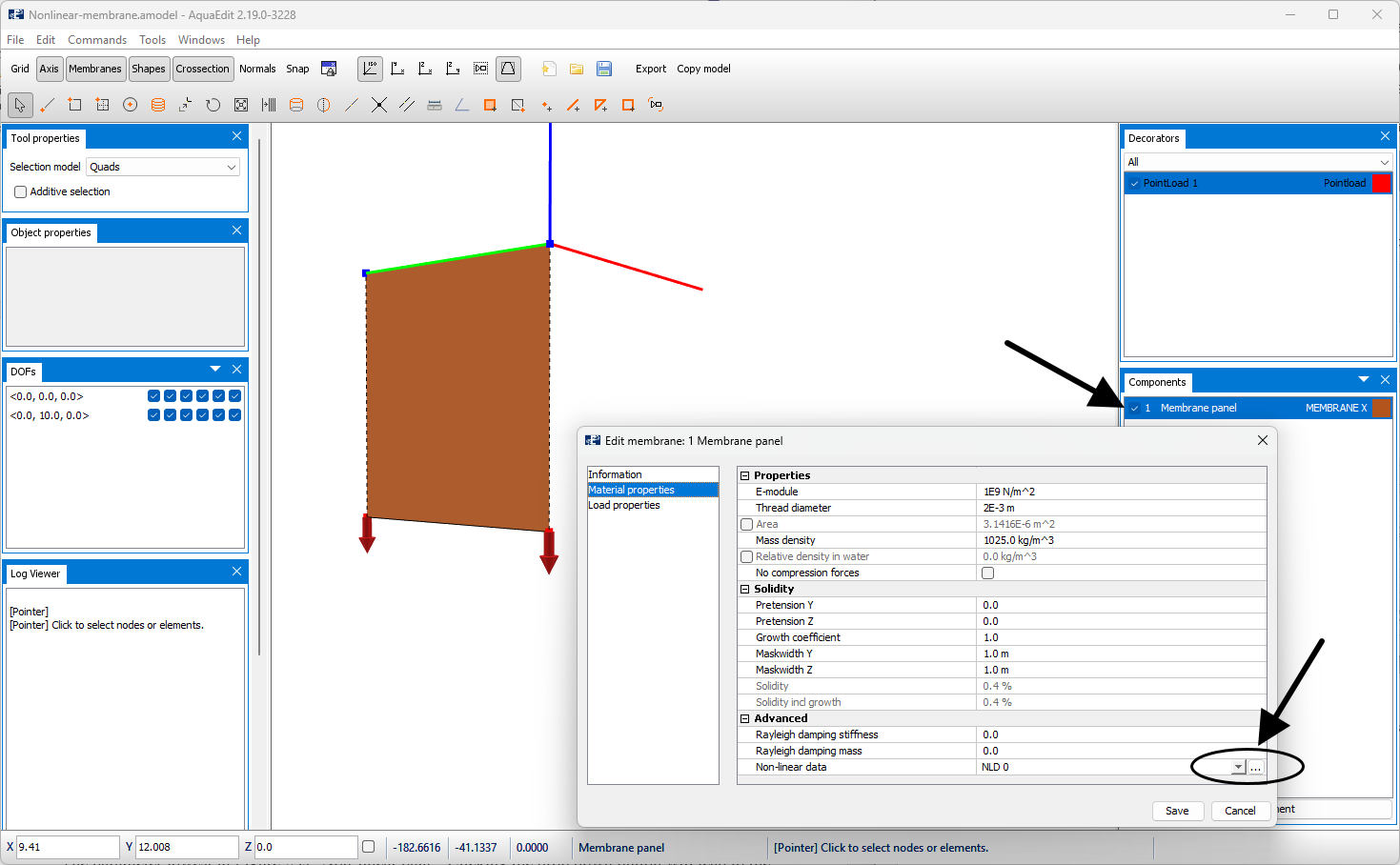
Choose the Material properties tab. The table for nonlinear data is found under Advanced. Select the three dots to the right, to open the prepared table.

Nonlinear data application

The prepared nonlinear table is called NLD0 and is viewed below.

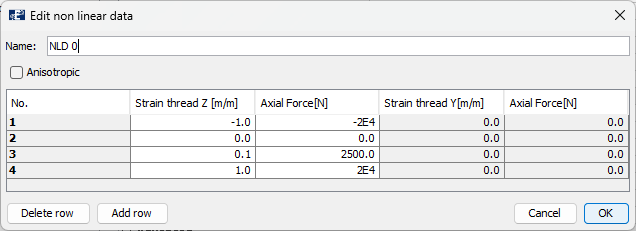
The following parameters are set when establishing nonlinear relations:

• Name: name of the table. Free of choice.
• Strain thread Z [m/m]: strain is unitless and defines the elongation per thread length. 1.0 means 1 meter per meter thread.
• Axial force [N]: force at the given strain.
• Anisotropic: if this check-box is ticket, one may establish nonlinear relations in both local Z- and Y- direction of the membrane. If not selected, it is assumed that the given relation is equal in both Y- and Z-direction.
• Delete row/ Add row: rows may be added or deleted.

Notes! The user should be aware of the following when establishing a nonlinear table:

• The strain-axial force relation should be increasing for increasing axial force.
• Depending on the loading situation, it could be wise to define relations below 0 as well. the ttttt
• Combinations of negative strain and positive axial force is not recommended.
• The table should be within the range of expected forces.
• If forces are lower than what is set as the lowest Axial force, the threads will bear the minimum force.
• If forces are higher than what is set as the highest Axial force, the threads will bear the maximum force.
• At least two rows are required to establish a nonlinear relation.

Given the force per vertical thread \(F_Z = -2500 \text{N} \) and the strain at this applied force will be \(\varepsilon = 0.1 \). The membrane elongation \(\Delta L \) becomes:

$$ (\Delta L = \varepsilon \cdot H = 0.1 \cdot 10 \text{m} = 1.0 \text{m}) $$

Analysis

Export your model to run an analysis. It is only necessary to run a static analysis, so Num total steps for waves can be set equal to 0.

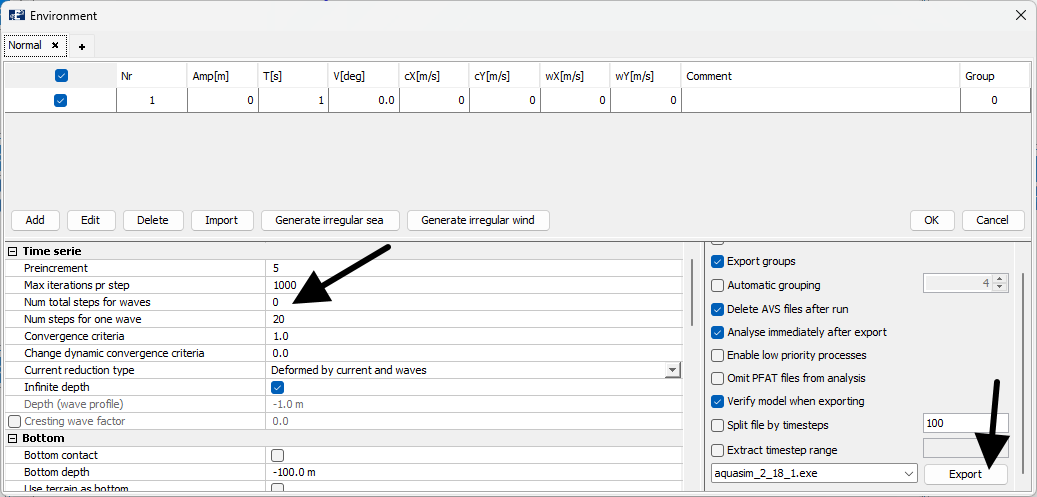
We named the analysis NLD_.

Results evaluation

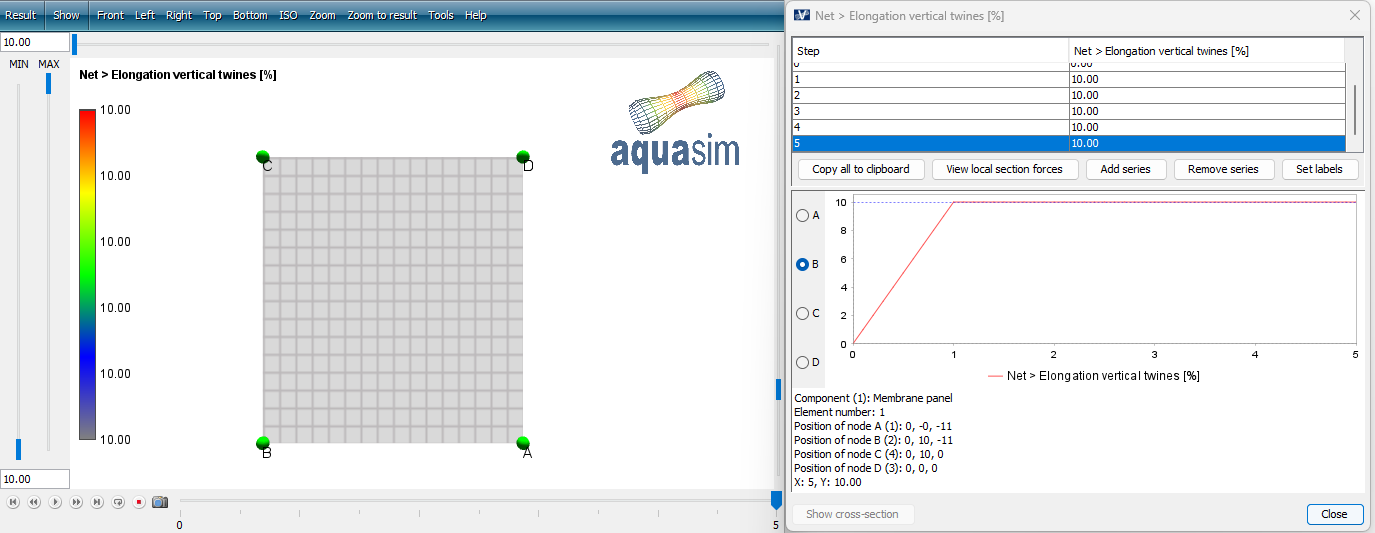
If you have not conducted your own analysis, you may open the NLD_01.avz following this tutorial. Load this file in AquaView. As seen from the results, the axial force in each vertical thread (twine) is 2500 N, this is in accordance with the calculated force, found in the table presented initially in this case study.

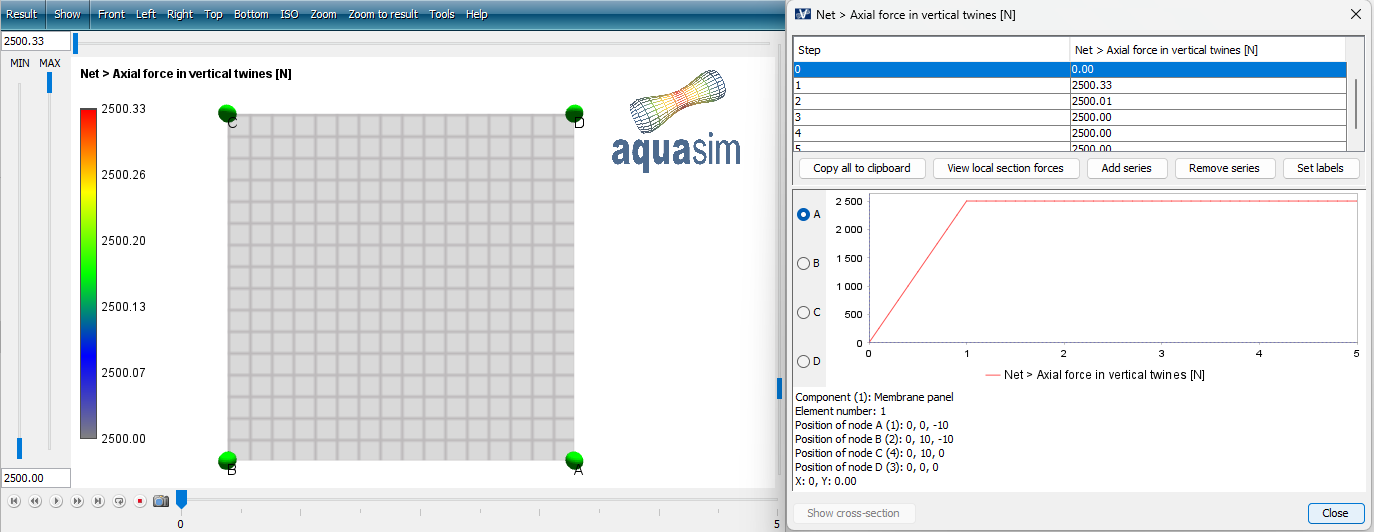
From the NLD0-table, it is defined that for 2500 N in axial force should give a strain of 0.1 m/m. The figure below shows the elongation of threads in the membrane, this is found from Result > Net > Elongation vertical twines [%]. This option presents the elongation of each thread in percent. The membrane has an original height of 10m, and 10% of this is 1m. The membrane is hence stretched 1 m downwards, this can also be seen by selecting Results > Displacement > Displacement Z [m].

Now that we see there is a logic connection between the input and results, we are ready to apply the NLD (nonlinear data) table to a physical model.

It should be noted that introducing nonlinear material properties will influence convergence of the analysis. Usually, it is more challenging to achieve convergence the more nonlinear the material behavior is.

Summary

In this tutorial you have been introduced to how nonlinear material properties can be applied to membrane components type Normal. A simple model is established in order to demonstrate the use, and how to validate input data in the nonlinear table.