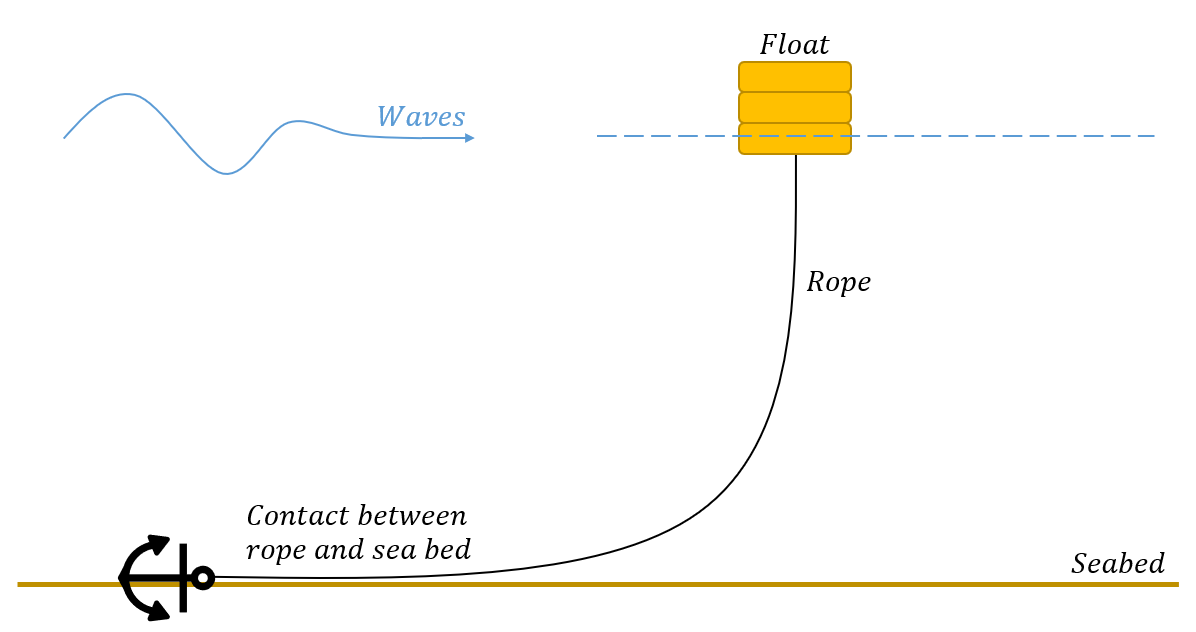
Consider a system consisting of a float. And a rope anchored to the seabed. The float is exposed to current and waves, which induces motion in the system. When the float moves up and down the rope will displace accordingly. The rope should be allowed to move freely upwards. When it is lowered, it will touch the seabed. The Displaced spring is hence applied with the purpose of rendering the contact between the rope and seabed.

In this case study you will determine the appropriate input values for spring type Displaced. First, you are to conduct static analyses to check your model and validate initial displacement with the spring. Then you should run a dynamic analysis with waves and current.

Principles of Spring: Displaced

In this section, basic principles of Spring: Displaced are explained. The main difference between Spring: Displaced and Bottom contact (found in the Export menu), is the possibility to model a seabed that is not flat. Displaced springs are assigned to nodes individually.

The Displaced amount of the node in z-direction is the basis for how the spring works. The user defines a maximum allowed displacement in z-direction (upwards or downwards) and a spring stiffness. The total displacement r of the node has the following relation:

$$ {r_{TOT} = r_0 + r_{Input} = {\sqrt [5]{\frac{F_z}{k_z }}}+Displaced amount}$$

where r₀ is the initial displacement due to gravitational force from the rope (or pipe etc.) and r_Input is the maximum allowed displacement of the node defined in AquaEdit in the field Displaced amount. Furthermore, k_z is the stiffness of the spring in z-direction. Spring stiffness can be applied for all degrees of freedom; translatory and rotational. Rotational stiffness will act as dynamic damping.