Lice skirts are modelled in AquaSim by applying the Lice skirt load formulation to membrane panels, as illustrated in Figure 1.

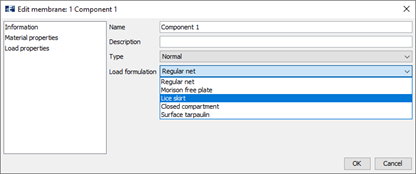
It should be noted that both waves and current contribute to loads from the drag coefficients, as outlined in the tutorial Lice skirt with current (Aquastructures AS, 2025a), since total velocity on the membrane panel is given by:

$${ U = U_c + U_w - U_s }$$

where

• \(U \quad \) is total velocity,
• \(U_c \quad \) is fluid velocity from current,
• \(U_w \quad \) is fluid velocity from wave motions,
• \(U_s \quad \) is the velocity of the membrane panel.

The magnitude of these loads is determined by the drag coefficients as presented in Figure 2.

Drag loads are calculated from the incident wave field and come in addition to the wave excitation loads.

Hydrodynamic forces and load formulations

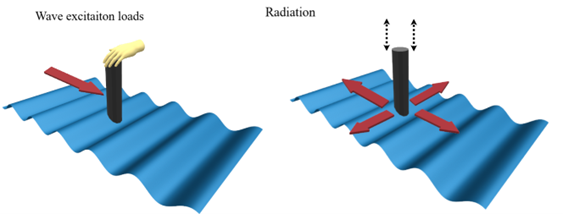
The aim of this section is to provide a short overview of the forces that arise on structures exposed to waves, to make the user capable of seeing the relation between input in AquaSim and its load formulations. Hydrodynamic loads in regular waves can be categorized into two main types: wave excitation loads and radiation loads.

$${ F_{\text{Hydro}} = F_{\text{EXC}} + F_{\text{RAD}} }$$

• Wave excitation loads originate from waves that impact a structure and are composed of Froude-Kriloff force \(F_{\text{FK}}\) and diffraction force \(F_{\text{DIFF}}\): $${ F_{\text{EXC}} = F_{\text{FK}} + F_{\text{DIFF}} }$$
• Radiation loads originate from the structure moving due to waves, and are normally expressed in terms of added mass and damping: $${ F_{RAD} = -F_{AddedMass} - F_{Damping} }$$

AquaSim provides several load formulations to calculate these forces, adapted for different types of structures and load scenarios. The next sections will elaborate on how the different load formulations work.

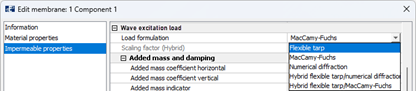
Wave excitation load formulations in AquaSim

Focus will be on the parameters found in the “Wave excitation load” section under Impermeable properties in AquaEdit (see Figure 4). Special attention is on “Flexible tarp” load formulation and its associated parameters (see Figure 5).

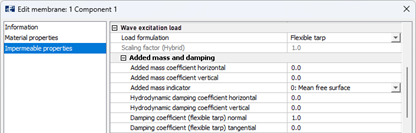
Associated parameters for Flexible tarp covers added mass and damping.

AquaSim has several load formulations to calculate wave excitation forces, these are shortly presented in Table 1.

Table 1

Aspects	Flexible tarp	MacCamy-Fuchs	Numerical diffraction	Hybrid flexible tarp / Numerical diffraction	Hybrid flexible tarp / MacCamy-Fuchs
Theory	Adapted for flexible woven textiles. Follows wave fluid particle motion.	Adapted for rigid structures. Applies theory from (R. MacCamy, 1954). Uses Bessel functions to model diffraction effects.	Numerical method NEMOH (A. Babarit, 2015) applied. Surface is discretized to calculate velocity potential (potential theory).	Combination of Flexible tarp and Numerical diffraction methods. The methods are weighted through “Diffraction scaling”.	Combination of Flexible tarp and MacCamy-Fuchs methods. The methods are weighted through “Diffraction scaling”.
Load terms included	Froude-Kriloff pressure.	Froude-Kriloff pressure and diffraction.	Froude-Kriloff pressure, diffraction, added mass and damping.	Weighted fraction of Froude-Kriloff (Flexible tarp) and Froude-Kriloff, diffraction, added mass and damping (Numerical diffraction).	Weighted fraction of Froude-Kriloff (Flexible tarp) and Froude-Kriloff and diffraction (MacCamy-Fuchs).
Limitations	Diffraction forces are omitted. Hence, this formulation is not suitable for rigid structures stand alone. Loads may be underestimated if applied structure is rigid. With option of adding radiation (added mass and damping) separately.	Fully rigid structures. Solves wave potential around a fixed, bottom mounted vertical cylinder in finite water depth. With option of adding radiation (added mass and damping) separately.	Handles complex geometries and multi-body interactions at finite water depth more flexible compared with analytical methods. Radiation forces are found automatically, meaning added mass- and damping coefficients works as scaling factor. Factors of 1.0 means the proposed solution from NEMOH is applied.	Accuracy depends on the structures rigidity/ flexibility and chosen scaling factor to weight the two methods.	Accuracy depends on the structures’ rigidity/ flexibility and chosen scaling factor to weight the two methods. With option of adding radiation (added mass and damping) separately.
Linear/ nonlinear	Linear but includes the nonlinear effect arising from in and out of water. Option to add the nonlinear velocity term in Bernoulli which means that the terms for calculation of mean drift are included except from the velocities originating from radiation.	Linear but includes the nonlinear effect arising from in and out of water, assuming small wave amplitudes and that fluid motion and pressure field vary linearly with wave amplitude. Corresponding option to add drift, as for Flexible Tarp.	Linear but includes the nonlinear effect arising from in and out of water, assuming linear waves. Corresponding option to add drift, as for Flexible Tarp.	Linear but includes the nonlinear effect arising from in and out of water. Corresponding option to add drift, as for Flexible Tarp.	Linear but includes the nonlinear effect arising from in and out of water. Corresponding option to add drift, as for Flexible Tarp.
Implementation	Analytical formulas	Analytical, closed form series	Numerical results calculated from NEMOH.	Analytical (Flexible tarp) and numerical (Numerical diffraction)	Analytical
Typical areas of application	For highly damping-dominated structures such as lice skirts, tarpaulins, tubes and so.	Stiff vertical cylinders, monopiles, other stiff floating containers.	Large volume structures, rigid bodies such as pontoons, barges, cages.	Semi-flexible structures attached to rigid structures.	Semi-flexible circular structures.