In this section, the principles of roller in AquaSim are explained. Rollers can be applied to Truss- and Beam elements. A principle sketch of how roller is defined is given in the figure below.

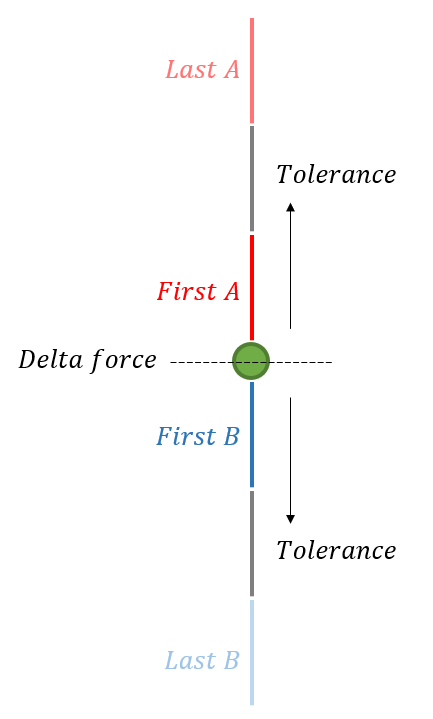
In AquaSim, rollers are applied to nodes as a node decorator. To define the range where the roller can slide, a first- and last-element is defined on each side of the roller. The first-elements A and B are automatically selected by AquaSim. The last-elements are where the roller will stop and can be edited by the user. When an analysis is run, AquaSim will compare the axial forces between A and B and adjust the length of the elements so that the forces are within the defined criteria. The analysis timestep will not converge until one or more of these criteria are satisfied.

The Delta force may be interpreted as a frictional resistance in the roller, and is the difference in axial force between element A and B:

$${Delta force = F_{Element A} - F_{Element B}}$$

When Delta force is assigned positive values, element A should have higher axial force than element B.

When Delta force is assigned negative values, element B should have higher axial force than element A.

Having defined a value for both Delta force and Tolerance, the timestep will not converge until the axial forces are within the Tolerance of the defined Delta force. If Delta force is 0, then the timestep will converge when the difference in axial force between element A and B are lower than the defined Tolerance.

During the iteration process, AquaSim will continuously try to establish equilibrium in axial forces between element A and B. Sometimes equilibrium can be challenging to achieve. Especially for cases when the distance between the first-element and last-element is large, or cases with large deformations. Stepping factor regulates how much the difference in axial force between element A and B can be adjusted before AquaSim moves on to the next iteration. The relation between axial force, element length and Stepping factor is:

$${PRE = {\frac{\Delta F \cdot Stepping factor}{EA}}}$$

Where PRE is the pre-strain in the element, ∆F is the difference in axial force between element A and B, E is the Elasticity modulus of the element and A is the cross-section area of the element.

Decrease stepping reduces the Stepping factor for each iteration. The relation between Stepping factor and Decrease stepping is:

$${Stepping factor \cdot \left({\frac{1}{\text{Iteration step} + 1 }}\right)^{\text{Decrease stepping}}}$$

Iteration step is the iteration to find equilibrium in the Roller system (not to be confused with the iteration of the time step). In addition, there are iterations for equilibrium at each stage, meaning that the total number of iterations can be large.

Note! The user should apply these two parameters with caution, it can enhance the risk of unstable analysis and divergent results. Generally, it is advised to apply the default values and seek other possibilities to achieve convergence in the roller system. Examples of such possibilities are presented later in this tutorial.